Citation
R Archibald, Jaron T Krogel, Paul RC Kent, "Gaussian process based optimization of molecular geometries using statistically sampled energy surfaces from quantum Monte Carlo", The Journal of chemical physics, 149(16), 2018.
Abstract
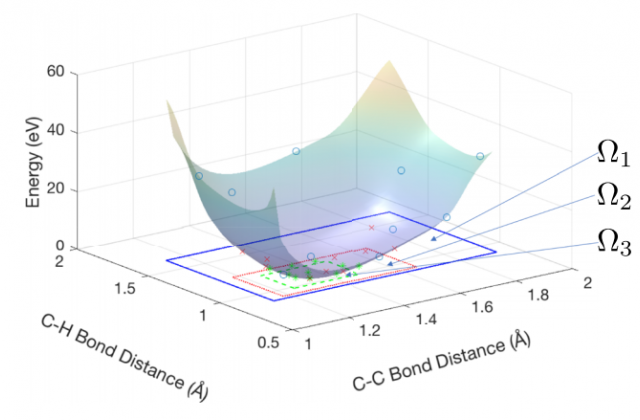
Optimization of atomic coordinates and lattice parameters remains a significant challenge to the wide use of stochastic electronic structure methods such as quantum Monte Carlo (QMC). Measurements of the forces and stress tensor by these methods contain statistical errors, challenging conventional gradient-based numerical optimization methods that assume deterministic results. Additionally, forces are not yet available for some methods, wavefunctions, and basis sets and when available may be expensive to compute to sufficiently high statistical accuracy near energy minima, where the energy surfaces are flat. Here, we explore the use of Gaussian process based techniques to sample the energy surfaces and reduce sensitivity to the statistical nature of the problem. We utilize Latin hypercube sampling, with the number of sampled energy points scaling quadratically with the number of optimized parameters. We show these techniques may be successfully applied to systems consisting of tens of parameters, demonstrating QMC optimization of a benzene molecule starting from a randomly perturbed, broken symmetry geometry.
Read PublicationLast Updated: May 28, 2020 - 4:06 pm