Achievement
A new adaptive hybrid meshfree discretization is devised for peridynamic models. A higher-order meshfree scheme is developed. The proposed scheme employs a weighted least squares based interpolation to analytically calculate spatial integrals using nodal values of collocation nodes, which is highly effective for linear models within spherical neighborhoods. To allow general implementation, the proposed scheme is combined with a standard meshfree scheme, which is more suitable to model material damage, within an adaptive framework. The effectiveness of the proposed discretization is demonstrated on brittle fracture and corrosion problems.
Significance and Impact
Material failure and damage modeling is an active area of research and a fundamental challenge for computational methods based on the classical continuum mechanics theory. Peridynamics overcomes this challenge by reformulating the classical continuum mechanics governing equation. However, the standard meshfree scheme commonly used for large-scale engineering peridynamics simulations can be highly computationally expensive and presents accuracy and convergence issues. The adaptive hybrid meshfree discretization proposed in this work allows for more accurate and less expensive peridynamics computations, while retaining the computational capabilities needed for fracture modeling.
Research Details
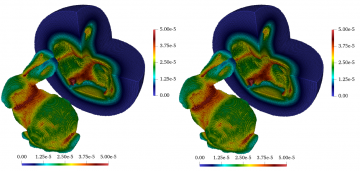
This paper proposes a meshfree scheme to discretize the nonlocal governing equation of peridynamics. The scheme is truly meshfree since it is free from any background cells to calculate spatial integrals. In the proposed scheme, within each peridynamic neighborhood, the main field variables of a problem are approximated through a collocation approach which employs a simple weighted least squares procedure. The bases of approximation are a complete set of monomials up to a predetermined order of consistency. The collocation is carried out over a subset of the family nodes called collocation nodes. The approximate field variables are directly plugged into the strong form of governing equations. In this way, for peridynamic neighborhoods with full compact support and governed by linear nonlocal models, an accurate quadrature rule is found. The collocation nodes are the corresponding quadrature points and the weights are computed without the need to calculate partial volumes involved in the standard particle-based scheme. We show that the proposed scheme can outperform the standard scheme in terms of efficiency. This lies in the fact that the proposed scheme makes use of a relatively small subset of family nodes to tackle the spatial integrations. In contrast, in the standard scheme, it is required to run over all the family nodes and apply a one-point quadrature within the background cell associated to each node. The efficiency of the proposed scheme is more significant in large-scale 3D problems with millions of degrees of freedom. Furthermore, in comparison to the standard scheme, the proposed scheme (even with the least order of consistency, C2) provides a higher level of accuracy and a proper convergence behavior in problems governed by smooth solutions. However, the advantages of the proposed scheme are valid as long as the problem, within the peridynamic neighborhood, can be well described by linear peridynamic models and approximated by smooth basis functions. To overcome this limitation, the proposed scheme is combined with the standard scheme using a hybrid (possibly adaptive) discretization. The hybrid discretization fully benefits from the advantages of both approaches to cope with challenging problems regarding dynamic fracture and corrosion. In the examples provided, we demonstrate that the hybrid approach can reproduce the solution given by the standard scheme at a much lower computational cost and significantly optimize the usage of computational resources.
Overview
Efficient and accurate calculation of spatial integrals is of major interest in the numerical implementation of peridynamics. The standard way to perform this calculation is a particle-based approach that discretizes the strong form of the peridynamic governing equation. This approach has rapidly been adopted by the peridynamics community since it offers some advantages. It is computationally cheaper than other available schemes, can conveniently handle material separation, and effectively deals with nonlinear peridynamic models. Nevertheless, peridynamic models are still computationally very expensive compared with those based on the classical continuum mechanics theory, particularly for large-scale problems in three dimensions. This results from the nonlocal nature of the peridynamics theory which leads to interactions of each node of a discretized body with multiple surrounding nodes. Here, we propose a new approach to significantly boost the numerical efficiency of peridynamics models. We propose a discretization scheme that employs a simple collocation procedure and is truly meshfree; i.e., it does not depend on any background integration cells. In contrast to the standard scheme, the proposed scheme requires a much smaller set of neighboring nodes (keeping the same physical length scale) to achieve a specific accuracy and is thus computationally more efficient. Our new scheme is applicable to the case of linear peridynamic models and within neighborhoods where the solution can be approximated by smooth basis functions. Therefore, to fully exploit the advantages of both the standard and the proposed schemes, a hybrid discretization is presented that combines both approaches within an adaptive framework. The high performance of the developed framework is illustrated by several numerical examples, including brittle fracture and corrosion problems in two and three dimensions.
To view the publication click here.
Last Updated: January 20, 2022 - 8:33 am