Achievement
A novel fully anisotropic formulation in bond-based peridynamics has been developed along with innovative reduced-order peridynamic models. The formulation can accommodate all material symmetry classes from classical linear elasticity. The reduced-order models are exact nonlocal analogues of classical two-dimensional planar elasticity models, specifically plane strain and plane stress models, which reduce a three-dimensional model to a two-dimensional representation. These peridynamic planar elasticity models provide a significant computational cost reduction while retaining the accuracy of reference three-dimensional peridynamic models. This work includes a new proof of the number of symmetry classes in two-dimensional classical linear elasticity and a generalization of known constraints in isotropic bond-based peridynamic models to the fully anisotropic setting.
Significance and Impact
The majority of peridynamic models are either isotropic or possess limited anisotropy. The proposed formulation allows to model any material symmetry class from classical linear elasticity in bond-based peridynamics, extending the bond-based peridynamic framework to a larger class of materials. The proposed two-dimensional peridynamic plane strain and plane stress models are directly derived from reference fully three-dimensional bond-based peridynamic models. In this way, a new mechanism for reduced-order representation is introduced that eliminates the need to calibrate peridynamic planar elasticity models.
Research Details
This paper has a twofold objective. First, it reviews pure two-dimensional, plane strain, and plane stress anisotropic models in classical linear elasticity. Second, it introduces novel formulations analogous to the classical models within the bond-based peridynamic theory of solid mechanics.
Our review of classical linear elasticity began with a new elementary and self-contained proof that there are exactly four material symmetry classes in classical linear elasticity in two dimensions: oblique, rectangular, square, and isotropic. Then, we presented pure anisotropic two-dimensional classical linear elasticity models for each of those symmetry classes. We further discussed planar approximations of three-dimensional anisotropic models in classical linear elasticity, specifically plane strain and plan stress formulations. The former normally concerns thick structures, whereas the latter often applies to thin plates. In three dimensions, there are eight material symmetry classes: triclinic, monoclinic, trigonal, orthotropic, tetragonal, transversely isotropic, cubic, and isotropic. Under certain assumptions, planar approximations reduce three-dimensional models to two-dimensional formulations. We reviewed plane strain and plane stress formulations in classical linear elasticity and specialized those formulations to the various symmetry classes. These two-dimensional approximations are based on decoupling in-plane and out-of-plane deformations which is achieved by assuming the material has a plane of reflection symmetry, i.e., the material symmetry is at least monoclinic. To discuss connections between the two-dimensional planar approximation models and the pure two-dimensional models in anisotropic classical linear elasticity, we reviewed engineering constants. It turns out that classical generalized plane stress models are equivalent, in terms of engineering constants, to pure two-dimensional models. In contrast, even though the classical plane strain models look identical to the pure two-dimensional models when expressed in terms of elasticity constants, they differ from the pure two-dimensional models, because the meaning of the elasticity constants varies upon the dimension. We finalized our review of classical linear elasticity with a discussion of Cauchy's relations in order to connect classical models to bond-based peridynamic models. While there is a single Cauchy's relation in two dimensions, there are six Cauchy's relations in three dimensions. Overall, Cauchy's relations reduce the number of independent constants in classical linear elasticity from 6 to 5, for general oblique models, and from 21 to 15, for general triclinic models.
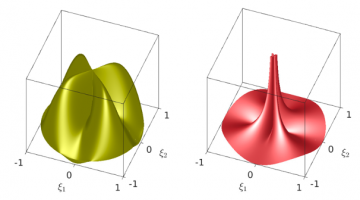
In the context of the bond-based peridynamic theory, we began by introducing new anisotropic models, which can accommodate all four material symmetry classes in two dimensions and discuss related micromodulus functions with corresponding visualizations. We then derived novel peridynamic plane strain and plane stress formulations. As opposed to common approaches for planar approximations in peridynamics, which are based on simply matching constants of two-dimensional peridynamic models to corresponding constants appearing in planar approximations in classical linear elasticity, our models directly apply peridynamic analogues of classical planar assumptions to reduce three-dimensional models to two-dimensional formulations. For this purpose, we resorted to three-dimensional anisotropic peridynamic models we developed. We discussed the resulting plane strain and plane stress micromodulus functions with corresponding visualizations, and we proved the convergence of our peridynamic plane strain and plane stress models to their counterparts in classical linear elasticity with imposed Cauchy's relations.
It is interesting to observe that, as opposed to peridynamic plane strain, which due to the thickness of the structure can simply consider points in the bulk of a body, peridynamic plane stress deals with thin plates and thus requires examination of surface effects. Furthermore, the peridynamic plane stress approximations result in a state-based peridynamic formulation.
The work presented in this paper offers a framework for simulation of two-dimensional problems based on the bond-based peridynamic theory, concerning all material symmetry classes found in classical linear elasticity. The newly introduced peridynamic plane strain and plane stress models provide means to reduce fully anisotropic three-dimensional bond-based peridynamic problems to two-dimensional formulations, resulting in significant computational savings, while retaining the dynamics of the original three-dimensional problems under proper assumptions.
Overview
This paper concerns anisotropic two-dimensional and planar elasticity models within the frameworks of classical linear elasticity and the bond-based peridynamic theory of solid mechanics. We begin by reviewing corresponding models from the classical theory of linear elasticity. This review includes a new elementary and self-contained proof that there are exactly four material symmetry classes of the elasticity tensor in two dimensions. We also summarize classical plane strain and plane stress linear elastic models and explore their connections to the pure two-dimensional linear elastic model, relying on the definitions of the engineering constants. We then provide a novel formulation for pure two-dimensional anisotropic bond-based linear peridynamic models, which accommodates all four material symmetry classes. We further present innovative formulations for peridynamic plane strain and plane stress, which are obtained using direct analogues of the classical planar elasticity assumptions, and we specialize these formulations to a variety of material symmetry classes. The presented anisotropic peridynamic models are constrained by Cauchy's relations, which are an intrinsic property of bond-based peridynamic models. The uniqueness of the presented peridynamic plane strain and plane stress formulations in this work is that we directly reduce three-dimensional models to two-dimensional formulations, as opposed to matching two-dimensional peridynamic models to classical plane strain and plane stress formulations. This results in significant computational savings, while retaining the dynamics of the original three-dimensional bond-based peridynamic problems under suitable assumptions.
To view the publication click here.
Last Updated: April 2, 2021 - 12:49 pm