Achievement
Selected for a Spotlight Talk (of Poster, Lightning (2 minute) Talk, and Spotlight (10 minute) Talk) at SubsetML Workshop @ ICML
Significance and Impact
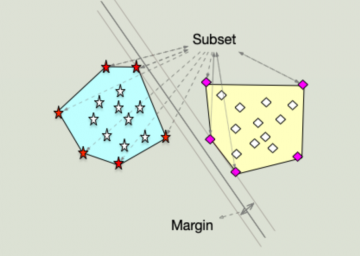
Labeled data which can be partitioned into classes by straight line classifiers is called linearly separable. Sometimes, linear classifiers can be trained in such a way that while the data is readily separated, the separating line falls needlessly close to the data (i.e., has a small margin.) This can lead to misclassification errors; if a linear separator falls near a data point, then test data can be near your training data set but fall on the far side of the linear separator. In the literature, larger margins are ensured by perturbing training data randomly in every direction via gaussian noise, and the new (auxiliary) data set is used to train the linear separator. The augmented data forms a sort of buffer for the original data. Hence, even if the separator falls near the augmented data there is a buffer between the separator and the original data set, thus ensuring larger classification margins. These methods increase the size of training data (at times exponentially), and correspondingly increase training times.
In this work, we detail a core set selection and augmentation technique based on discrete geometric properties which assure larger margins while decreasing the size of training data and improving classification margins. We prove that these techniques work in the case of linear separators, and show (empirically) that they also yield faster training time on smaller data sets with increased accuracy for simple neural net architectures on the MNIST data set.
Research Details
The critical observation is that if a linear separator is near one class of a labeled data set, then it is necessarily near an extreme point of the convex hull of said class of data. Hence, the previously studies methods for data augmentation can be performed on a small subset of the given data- namely the extreme points of the class. Hence, if one can compute the extreme points of a convex hull quickly, and if the extreme points constitute a small (say logarithmic) portion of the larger data set, then even if the augmentation scheme yields exponentially many augmented points, the augmented set is on the order of the original data set and training time does not increase. However, the margins are assured to be increased, and misclassification error drops. Unfortunately, the QuickHull algorithm (while polynomial in pointset size for fixed dimension) is exponential in dimension. However, we can demonstrate that distance preserving random projections (Johnson-Lindenstrauss e.g.,) map extreme points to near extreme points, and so by projecting to a low dimension and then performing an extreme point computation still leads to a better classification margin on an augmented data set. When applied to the MNIST data set, we saw an augmented data set which was as low as 30% the size of the original data with an increase in test accuracy.
We have further seen empirically that with a simple neural network classifier, the augmented data set output by our randomized projection/discrete geometric coreset selection scheme yields an increase in test accuracy for the MNIST dataset.
Note: The authors share first authorship equally.
Last Updated: August 17, 2021 - 12:15 pm