Achievement
The nonlinear filtering problem is one of the key missions in data assimilation, in which observations of a system are incorporated into the state of a numerical model of that system. Mathematically, the nonlinear filtering problem is to obtain, recursively in time, the best estimate of the state of unobservable stochastic dynamics S = {St : t ≥ 0}, based on an associated observation process, M = {Mt : t ≥ 0}, whose values are a function of S after corruption by noises. This suggests the optimal filtering problem of obtaining the conditional distribution of the state St from the observations up until time t, which achieves the best estimate of this distribution, in the squared error sense, based on the available observations.
Significance and Impact
We develop a novel numerical method for solving the nonlinear filtering problem of jump diffusion processes. The methodology is based on numerical approximation of backward stochastic differential equation systems driven by jump diffusion processes and we apply adaptive meshfree approximation to improve the efficiency of numerical algorithms. We then use the developed method to solve atom tracking problems in material science applications. Numerical experiments are carried out for both classic nonlinear filtering of jump diffusion processes and the application of nonlinear filtering problems in tracking atoms in material science problems.
Research Details
- Develop an efficient Backward SDE filter for jump diffusion processes.
- Introduce the potential application of the developed algorithms in material sciences.
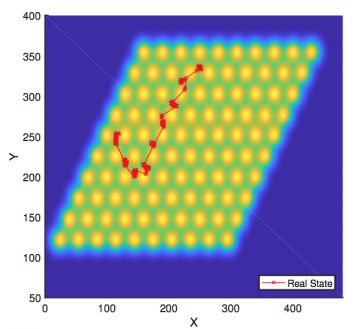
- Demonstrate Backward SDE filter in material sciences and demonstrate the effectiveness of the Backward SDE filter in tracking atom trajectories on two different material surfaces.
Overview
The connection between forward backward doubly stochastic differential equations and the optimal filtering problem is established without using the Zakai's equation. The solutions of forward backward doubly stochastic differential equations are expressed in terms of conditional law of a partially observed Markov diffusion process. It then follows that the adjoint time-inverse forward backward doubly stochastic differential equations governs the evolution of the unnormalized filtering density in the optimal filtering problem.
Citation
Richard Archibald, Feng Bao, Peter Maksymovych, "Backward SDE Filter for Jump Diffusion Processes and Its Applications in Material Sciences", arXiv preprint arXiv:1805.11038, 2018
Last Updated: January 15, 2021 - 2:15 pm