Achievement
We have proposed an efficient, fully implicit scheme for solving simplified Boltzmann-Poisson systems, and compared iterative solvers for two different fixed-point formulations of these systems on silicon diode problems with various electron mean-free-path.
Significance and Impact
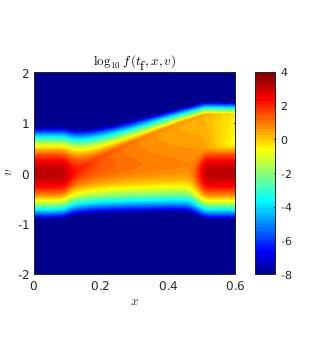
The proposed fully implicit numerical scheme is applied to solve models of free electron movement in semiconductor devices under a low-density assumption. This scheme allows for efficient solutions to multiscale problems with large-scale variations in the electron mean-free-path, which are usually challenging for standard explicit or implicit-explicit (IMEX) schemes. Four iterative solvers and their accelerated variants are considered in the implicit update. The performance of these solvers has been compared on problems modelling semiconductor devices with various electron mean-free-path. These numerical results provide a guideline on the selection of iterative solvers for problems with different material profiles. The proposed scheme can also be applied to charged particle transport simulation in different areas.
Research Details
• Developed fully implicit scheme for solving simplified Boltzmann-Poisson systems for semiconductors.
• Investigated two types of fixed-point formulation of implicit updates: one can be solved in a single strongly coupled iterative loop and the other one requires two nested iterative loops.
• Compared the performance of several iterative fixed-point solvers on the two types of problems with various levels of collisionality.
Overview
Several different approaches are proposed for solving fully implicit discretizations of a simplified Boltzmann-Poisson system with a linear relaxation-type collision kernel. This system models the evolution of free electrons in semiconductor devices under a low-density assumption. At each implicit time step, the discretized system is formulated as a fixed-point problem, which can then be solved with a variety of methods. A key algorithmic component in all the approaches considered here is a recently developed sweeping algorithm for Vlasov-Poisson systems. A synthetic acceleration scheme has been implemented to accelerate the convergence of iterative solvers by using the solution to a drift-diffusion equation as a preconditioner. The performance of four iterative solvers and their accelerated variants has been compared on problems modeling semiconductor devices with various electron mean-free-path.
Last Updated: January 15, 2021 - 4:56 pm