A sparse-grid probabilistic scheme for approximation of the runaway probability of electrons in fusion tokamak simulation

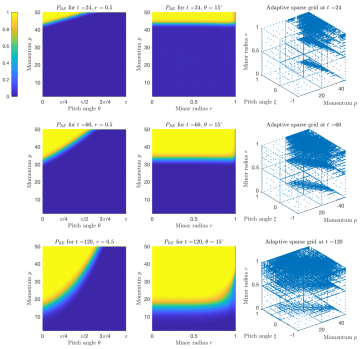
Runaway electrons (RE) generated during magnetic disruptions present a major threat to the safe operation of plasma nuclear fusion reactors. A critical aspect of understanding RE dynamics is to calculate the runaway probability, i.e., the probability that an electron in the phase space will runaway on, or before, a prescribed time. Such probability can be obtained by solving the adjoint equation of the underlying Fokker-Planck equation that controls the electron dynamics. In this effort, we present a sparse-grid probabilistic scheme for computing the runaway probability. The key ingredient of our approach is to represent the solution of the adjoint equation as a conditional expectation, such that discretizing the differential operator reduces to the approximation of a set of integrals. Adaptive sparse grid interpolation is utilized to approximate the map from the phase space to the runaway probability. The main novelties of this effort are the integration of the sparse-grid method into the probabilistic numerical scheme for computing escape probability, and the application of the proposed method in computing RE probabilities. Two numerical examples are given to illustrate that the proposed method can achieve O(∆t) convergence, and that the local anisotropic adaptive refinement strategy can effectively handle the sharp transition layer between the runaway and non-runaway regions.

Publication:

• M. Yang, G. Zhang, D. del-Castillo-Negrete, M. Stoyanov, and M. Beidler, A sparse-grid probabilistic scheme for approximation of the runaway probability of electrons in fusion tokamak simulation, Springer Lecture Notes on CS&E, 2020 (https://arxiv.org/abs/2001.05800).