Achievement
Researchers at Oak Ridge National Laboratory (ORNL) designed a label-propagation algorithm that computes the connected components in a graph while being tolerant to errors. The algorithm relies on the self-stabilization concept, which means that an incorrect state introduced by an error is corrected by the algorithm by reaching a correct state in a finite number of steps. Self-stabilization may require an algorithm to perform additional computation and use additional memory or storage. The developed self-stabilizing label-propagation algorithm performs O (V log V) additional computation and requires O (V) additional storage over its conventional counterpart. It vastly outperforms traditional approaches, such as triple modular redundancy.
Significance and Impact
Resilience, i.e., obtaining a correct solution in a timely and efficient manner, is a key challenge in extreme-scale supercomputers. Supercomputer hardware, from time to time, encounters an error that remains undetected until it is too late and an application has been impacted by data corruption. Computational algorithms used by the US Department of Energy’s supercomputers need to be resilient against such errors to ensure the trust in their results and to not negatively impact science breakthroughs by requiring multiple simulations to assure correctness. The developed self-stabilizing label-propagation algorithm to compute the connected components in a graph is resilient to such errors and outperforms traditional approaches for providing such level of resilience.
Research Details
- Developed a self-stabilizing label-propagation algorithm to compute the connected components in a graph
- Identified the valid and invalid states of this algorithm were identified
- Studied the self-stabilizing property to reach a valid state from an invalid state
- Identified the computational and storage complexity of the developed algorithm
- Experimentally evaluated the resilience and performance of the developed algorithm
Publication
Piyush Sao, Chistrian Engelmann, Srinivas Eswar, Oded Green, and Richard Vuduc. Self-stabilizing Connected Components. In Proceedings of the 32nd International Conference on High Performance Computing, Networking, Storage and Analysis (SC) Workshops 2019: 9th Workshop on Fault Tolerance for HPC at eXtreme Scale (FTXS) 2019, Denver, CO, USA, November 22, 2019. IEEE Computer Society, Los Alamitos, CA, USA.
Overview
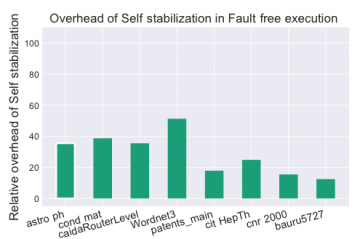
For the problem of computing the connected components of a graph, this work considers the design of algorithms that are resilient to transient hardware faults, like bit flips. More specifically, it applies the technique of self-stabilization. A system is self-stabilizing if, when starting from a valid or invalid state, it is guaranteed to reach a valid state after a finite number of steps. Therefore on a machine subject to a transient fault, a self-stabilizing algorithm could recover if that fault caused the system to enter an invalid state. We give a comprehensive analysis of the valid and invalid states during label propagation and derive algorithms to verify and correct the invalid state. The self-stabilizing label-propagation algorithm performs O (V log V) additional computation and requires O (V) additional storage over its conventional counterpart (and, as such, does not increase asymptotic complexity over conventional). When run against a battery of simulated fault injection tests, the self-stabilizing label propagation algorithm exhibits more resilient behavior than a triple modular redundancy (TMR) based fault-tolerant algorithm in 80% of cases. From a performance perspective, it also outperforms TMR as it requires fewer iterations in total. Beyond the fault-tolerance properties of self-stabilizing label-propagation, we believe, they are useful from the theoretical perspective; and may have other use-cases.
Last Updated: January 15, 2021 - 11:31 am