Achievement
Created performance models for designing multiresilient iterative high-performance computing (HPC) applications. Demonstrated the design of a performance efficient and multiresilient linear solver application using checkpoint-based recovery and non-ideal soft error detection.
Significance and Impact
Design patterns and their performance models guide developers to design and deploy scientific applications on HPC systems to reach accurate solutions in a timely and efficient manner. The systematic exploration of the resilience-performance trade-off design space using multiple resilience design patterns provides optimal end-to-end application performance based on desired user specifications.
Research Details
- Created performance models for efficient design of multiresilient iterative algorithms considering the interaction between non-ideal soft error detection and checkpoint-based recovery
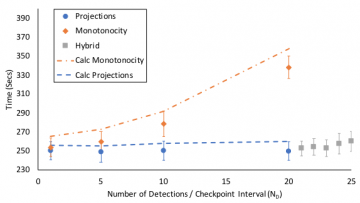
- Compared the resilience and performance impacts due to the use of two distinct soft error detectors in a GMRES solver: one detector has high accuracy and high overhead, whereas the other detector has low accuracy and low overhead.
- Explored the performance-resilience trade-off space created by the type and frequency with which soft error detection is performed inside each checkpoint interval.
Overview
High performance computing (HPC) applications are affected by multiple types of errors occurring in HPC systems which hinder with their ability to make forward progress and their correctness. The errors are broadly categorized into soft errors causing silent data corruption (SDC) and hard errors causing process failures or a fatal application crashes. Multiresilience is the ability to tolerate and maintain forward progress in presence of both soft errors and process failures.
In this work, checkpoint-based recovery is demonstrated to provide multiresilience by performing multiple soft error detections before the checkpoint to limit the propagation of soft errors in iterative HPC applications. The use of resilience design patterns enables systematic integration of multiple independent techniques which encapsulate detection, containment, and mitigation of each error type with minimal impact on application performance. The design patterns provide a generalizable solution to a recurring problem. We navigate the performance-resilience tradeoff space by evaluating the overall time to solution of multiple multiresilience solutions in a linear solver application.
Specifically, we evaluate two distinct type of soft error detectors in our work, one has high accuracy and high overhead, and other one has low accuracy and low overhead. In both cases, we assume that some soft errors can go undetected causing the iterative algorithm to take additional iterations to converge to a solution beyond the error-free case. The frequency with which the soft error detections are employed represents a tradeoff between the overhead of the detector in the error-free case and the extra work required for convergence.
For example, the high accuracy detector can lower the overheads due to additional iterations but the overhead of using the detector itself can be high. This tradeoff can be explored with the aid of performance models proposed in this work, which have been evaluated using statistical fault injection experiments. In our experiments with a GMRES-based linear solver application, we find a hybrid detector which combines the use of low accuracy detector at high frequency and high accuracy detector at low frequency is observed to have comparable resiliency as using the high accuracy detector at highest frequency with significantly less impact on performance.
Last Updated: May 28, 2020 - 4:05 pm