Achievement
Researchers at ORNL have developed new solvers for implicit time discretization of a non-linear electron transport model.
Significance and Impact
Kinetic equations are important for simulating charged-particle transport in physical regimes that are relevant to nanoscale electronic devices, as well as fusion plasmas in tokamaks. For extreme multiscale problems, the new approach yields order-of magnitude improvements in efficiency when compared to more conventional time discretization techniques.
Research Details
The algorithm relies on
- a memory-efficient solver for large non-linear transport equations;
- a sweeping algorithm that accelerates the solver by tracking electron trajectories;
- and reduced-order fluid models for preconditioning in asymptotic regimes.
Overview
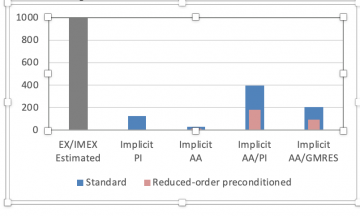
Researchers from Oak Ridge National Laboratory and the University of Massachusetts Dartmouth investigated several different approaches for solving fully implicit discretizations of a simplified Boltzmann-Poisson system with an approximate collision operator that describes linear relaxation. This system models the evolution of free electrons in semiconductor devices under a low density assumption. The proposed fully implicit scheme allows for efficient solutions to multiscale problems with large-scale variations in the electron mean-free-path, which are usually challenging for standard explicit or implicit-explicit schemes. At each implicit time step, the discretized system is formulated as a fixed-point problem, which can then be solved with a variety of methods.
A key algorithmic component in all the approaches considered here is a recently developed sweeping algorithm for Vlasov-Poisson systems, a collisionless variant of the Boltzmann-Poisson system considered in this work. Four iterative solvers and their preconditioned variants are considered in the implicit update. The performance of these solvers has been compared on problems modeling semiconductor devices with various electron mean-free-path. These numerical results provide a guideline on the selection of iterative solvers for problems with different material profiles.
This material was based upon work supported by the Office of Advanced Scientific Computing Research (ASCR) and performed at the Oak Ridge National Laboratory (ORNL). ORNL is operated by UT-Battelle, LLC., for the U.S. Department of Energy under Contract DE-AC05-00OR22725.
Last Updated: January 14, 2021 - 8:03 pm