Achievement
A new elementary, self-contained, and complete proof is derived showing that there are exactly four symmetry classes of the elasticity tensor in two-dimensional linear elasticity.
Significance and Impact
Many materials exhibit symmetry in their material response, which can be captured to a certain degree in linear elasticity by imposing symmetry on the elasticity tensor. Imposing such symmetry is also necessary for dimension-reducing approximations such as plane strain, plane stress, and axisymmetry. However, the elasticity tensor is only capable of describing a rather limited number of symmetry classes. This work provides a complete proof of the number of those symmetry classes in two dimensions, while presenting the proof in an accessible form to a broad audience.
Research Details
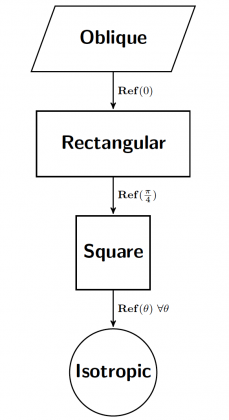
The objective of this paper is to present a new, elementary, and self-contained proof that there are exactly four symmetry classes of the elasticity tensor in two-dimensional linear elasticity: oblique, rectangular, square, and isotropic. This is accomplished by an exhaustive search for the subgroups generated by reflection symmetry transformations and then showing that the set of those groups is closed under the introduction of rotation symmetry transformations. We identify the sets of transformations (rotations and reflections) for each symmetry class. It is interesting to note that unlike for the elasticity tensor in three dimensions, in two dimensions the symmetry group of the elasticity tensor cannot be characterized entirely by rotation transformations. Lastly, as a convenient reference, we present the anisotropic two-dimensional classical linear elasticity models for each of the symmetry classes.
Overview
We present an elementary and self-contained proof that there are exactly four symmetry classes of the elasticity tensor in two dimensions: oblique, rectangular, square, and isotropic. In two dimensions, orthogonal transformations are either reflections or rotations. The proof is based on identification of constraints imposed by reflections and rotations on the elasticity tensor, and it simply employs elementary tools from trigonometry, making the proof accessible to a broad audience. For completeness, we identify the sets of transformations (rotations and reflections) for each symmetry class and report the corresponding equations of motions in classical linear elasticity.
To view the publication click here.
Last Updated: June 15, 2022 - 9:55 am