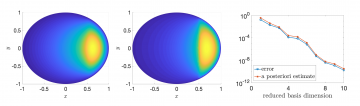
Parameter variability of the model with respect to different fractional exponents (left & middle). The error of the reduced model and error estimates (right).
Achievement
Researchers at ORNL have developed a learning-based approximation strategy to accelerate parameter studies for non-classical models of diffusion.
Significance and Impact
Non-classical models of diffusion are being used to advance our understanding of materials and transport processes and to improve image analysis. While these models reflect certain phenomena better than their classical counterparts, they also come with a higher computational cost. By reducing computational time, the proposed strategy enables practical application of such models for large-scale tasks such as optimization, design, and uncertainty quantification.
Research Details
The developed method:
- Relies on rigorous understanding of model behavior as a function of the parameter choice
- Enables significant computational speed-up by inferring the most important information in advance (offline),
- Constructs a cheap surrogate model for fast evaluations (online).
- Guarantees accuracy with certified error bounds.
Overview
Nonlocal models are a broad category of mathematical models which arise in many areas of science, such as, e.g., solid and fluid mechanics, contact mechanics, subsurface flows, and image analysis. The corresponding nonlocal diffusion operators are used to describe anomalous diffusion processes, with a prominent example given by the fractional Laplacian. While nonlocal models better reflect many physical processes, the precise model parameters are unknown in many practical applications. In this case, one requires not only to approximate the solution as a function of the spatial variable, but also as a function of the model parameters. To enable a computationally efficient exploration of the parametric manifold, we develop an algorithmic framework based on the affine approximation of the nonlocal kernel by local polynomials and the reduced basis method. Here, a particular focus is placed on the fractional Laplace equation, with the fractional exponent and nonlocal interaction radius being the model parameters. As a byproduct of the analysis, we establish new parametric regularity results, which are of independent interest for other applications, such as optimization or parameter inference. As a certification of the method, we provide reliable a posteriori error estimates and establish an exponential convergence rate, which is also supported by the numerical experiments.
Last Updated: January 14, 2021 - 8:16 pm