Low-Memory, Discrete Ordinates, Discontinuous Galerkin Methods for Radiative Transport

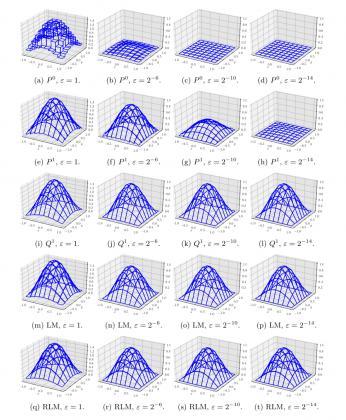
The discrete ordinates discontinuous Galerkin (SN -DG) method is a well-established and practical approach for solving the radiative transport equation. In this paper, we study a low- memory variation of the upwind SN -DG method. The proposed method uses a smaller finite element space that is constructed by coupling spatial unknowns across collocation angles, thereby yielding an approximation with fewer degrees of freedom than the standard method. Like the original SN - DG method, the low-memory variation still preserves the asymptotic diffusion limit and maintains the characteristic structure needed for mesh sweeping algorithms. While we observe second-order convergence in the scattering dominated, diffusive regime, the low-memory method is in general only first-order accurate. To address this issue, we use upwind reconstruction to recover second-order accuracy. For both methods, numerical procedures based on upwind sweeps are proposed to reduce the system dimension in the underlying Krylov solver strategy.