Improvements to a class of hybrid methods for radiation transport: Nyström reconstruction and defect correction methods

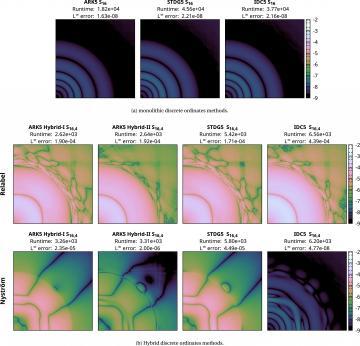
In this paper, two modifications are introduced for improving the accuracy, versatility, and robustness of a class of hybrid methods for radiation transport.  Such ethods are constructed by splitting the radiative flux into collided and uncollided components to which low- and high-resolution angular approximations are applied, respectively. In this work we focus on discrete ordinates discretizations of high and low order. The first modification we introduce changes the way in which the collided component is mapped into the uncollided component at the end of each time step in a simulation. The new mapping is a Nyström-type reconstruction that is applicable to arbitrary discrete ordinates quadratures, is guaranteed to preserve positivity of the solution provided that all ordinate weights are positive, is significantly more accurate than previous methods, and can be readily extended to other discretizations such as moment methods, finite element methods, and diffusion approximations. The second modification leverages integral deferred correction (IDC) to iteratively correct for the splitting error introduced by the inconsistency in angular discretization between the collided and uncollided components, in addition to improving the accuracy of the low-order temporal error that is treated by traditional IDC methods.  Numerical tests in one- and two-dimensional geometries are used to demonstrate the increased accuracy and efficiency of the proposed modifications.  It is found that the two techniques combined yield methods with solution accuracy and memory requirements comparable to that of monolithic discrete ordinates methods while reducing runtime by as much as a factor of between two and ten, depending on the problem.