Achievement
A general state-based peridynamics model for multiphase, multicomponent flow of non-Newtonian and compressible fluids is developed to simulate transport of fluids in an arbitrary heterogeneous porous medium.
Significance and Impact
The formulation presented in this work, combined with a peridynamics-based damage model, can be used to simulate hydraulic fracturing with complex fluids.
Research Details
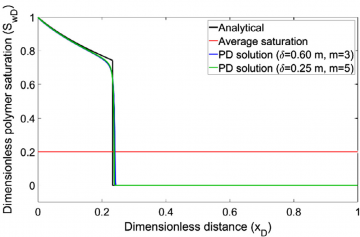
We present a general state-based peridynamic formulation for multiphase, multicomponent fluids showing varying compressibility and non-Newtonian behavior. The model is specialized to different kinds of multiphase models used in petroleum engineering, specifically black-oil and immiscible two-phase flow models. We demonstrate application of the multiphase model by solving a one-dimensional linear, immiscible displacement of oil by water (water flood) and by a shear-thinning polymer (polymer flood). The proposed model captures saturation profiles and recovers given analytical local solutions in the local limit. In the polymer flood problem, simulations also capture the observation that oil recovery decreases at higher injection rates of a shear-thinning polymer.
Overview
A general state-based peridynamics model is developed to simulate transport of fluids in an arbitrary heterogeneous porous medium. The generality encompasses modeling of multiphase, multicomponent flow of non-Newtonian and compressible fluids, which is often encountered in but not limited to subsurface reservoirs. Peridynamics is especially useful for solving non-local problems, such as crack propagation, since it does not assume spatial continuity of field variables. Thus, the formulation presented in this work, combined with a peridynamics-based damage model, can be used to simulate hydraulic fracturing with complex fluids. To demonstrate its capability to simulate multiphase flow in porous media, the derived model is verified against the analytical Buckley-Leverett solution for immiscible Newtonian two-phase flow. Furthermore, the non-Newtonian two-phase fluid flow in porous media is verified by simulating the polymer flood process involving an immiscible displacement of a Newtonian fluid by a non-Newtonian fluid against a generalized solution. The non-local solutions are shown to be consistent with the corresponding local solutions in limiting cases. Moreover, mass conservation of all the phases is satisfied, irrespective of discretization and extent of non-locality.
To view the publication click here.
Last Updated: January 15, 2021 - 11:26 am