Achievement
- We proposed a framework to extend existing feasible-start algorithms tailored for inequality-constrained convex quadratic programs (CQPs) to handle general CQPs with infeasible starting points via an exact penalty function approach.
- We proved global convergence and provided infeasibility certificate under mild assumptions on the CQPs, with some general requirements on the feasible-start algorithm and penalty-parameter updating rule.
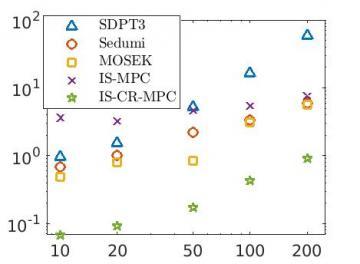
- Promising numerical results are reported on both randomly generated problems and support-vector machine classifier training problems in comparison with popular codes.
Significance and Impact
Many sophisticated solvers have been proposed for optimization problems of the form of convex quadratic programs (CQPs). While a feasible starting point is usually required by optimization solvers, it is often not readily available in practice. In this case, obtaining a feasible starting point usually requires solution to an auxiliary problem, which is computationally inefficient. For arbitrary user-provided feasible-start inequality-constrained CQP solvers, we proposed a framework that
- enables the application of feasible-start CQP solvers on problems where feasible starting points are unavailable;
- extends CQP solvers tailored for inequality-constrained CQPs to handle problems with equality constraints;
- provides an certificate of infeasibility at a negligible additional cost when solving primal-infeasible CQPs.
Global convergence is guaranteed on general CQPs when the user-provided CQP solvers equip rather basic properties such as feasibility, eventual descent, and convergence. Numerical results show that the framework successfully extends efficient CQP solvers to a broader class of problems with minor additional cost.
Research Details
An exact-penalty-based framework for allowing for infeasible starts in solving CQPs (including linear optimization problems) was proposed and analyzed. Global convergence of the framework is shown for any user-provided feasible, eventual descent, and convergent base CQP solvers. With negligible additional computational cost per iteration, an infeasibility test is included that provides an infeasibility certificate when the problem at hand is indeed infeasible. The framework was tested on constrained-reduced Mehrotra's predictor-corrector (CR-MPC) solver. Numerical results suggest that, on imbalanced CQPs, infeasible-start CR-MPC is significantly faster than SDPT3, SeDuMi, and MOSEK. It is also confirmed that constraint reduction is very powerful on such problems.
Overview
A framework is proposed for solving general convex quadratic programs (CQPs) from an infeasible starting point by invoking an existing feasible-start algorithm tailored for inequality-constrained CQPs. The central tool is an exact penalty function scheme equipped with a penalty-parameter updating rule. The feasible-start algorithm is merely required to satisfy certain general requirements, and so is the updating rule. Under mild assumptions, the framework is proved to converge on CQPs with both inequality and equality constraints and, at negligible additional cost per iteration, produces an infeasibility certificate, together with a feasible point for an (approximately) l1-least relaxed feasible problem when the given problem does not have a feasible solution. Numerical comparison with popular codes is reported on both randomly generated problems and support-vector machine classifier training problems. The results show promise.
Last Updated: January 15, 2021 - 11:28 am