Achievement
Researchers at ORNL and collaborating universities have designed a new class of error-inhibiting time discretization techniques that improve the accuracy of standard schemes.
Significance and Impact
- Increased rates of convergence over base methods that lead to significant reduction in errors for the same computational effort.
- Demonstrated improvements in accuracy for a variety of test problems, including convection-dominated flows with shocks and nonlinear problems that feature dynamics at multiple scales (such as the Van der Pol oscillator).
- Simple, faster, and more accurate time-stepping alternatives for developers working on the Energy Exascale Earth System Model (E3SM) Project.
Research Details
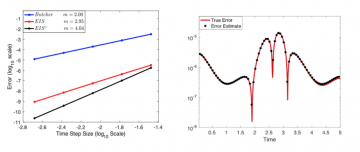
- Suppressed error accumulation during the course of a simulation
- Applied a simple postprocessing procedure at the end of a simulation.
- Enabled adaptivity and reduce communication costs by using low-cost error estimator
Overview
Researchers including ORNL’s Zachary Grant introduce a new approach to analyzing the accumulation of errors when evolving the solution of time dependent problems, allowing for the design of new higher-order methods while requiring a smaller computational footprint. These new schemes have shown an improvement of two orders of accuracy compared to traditional methods for similar amounts of work. The two follow up papers demonstrate that this analysis not only works for classical ODE methods, but for more sophisticated ones as well including but not limited to multi-derivative time discretization and additive time-stepping strategies. All methods were designed to optimize the efficiency of the scheme with respect to a desired order of accuracy by considering both linear stability and strong stability-preserving capabilities.
Last Updated: January 14, 2021 - 7:59 pm