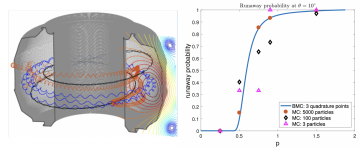
RIGHT: Our method (blue curve) with 3 particles achieves the same accuracy as MC methods with 5000 particles (red dots). Our method’s cost (the same as MC with 3 particles) is only 0.06% of the cost of MC with 5000 particles.
Achievement
Kinetic descriptions of runaway electrons (REs) are usually based on Fokker-Planck models that determine the probability distribution function of REs in 2-dimensional momentum space. Despite the simplification involved, the Fokker-Planck equation can rarely be solved analytically and direct numerical approaches [e.g., continuum and particle-based Monte Carlo (MC)] can be time consuming, especially in the computation of asymptotic-type observables including the runaway probability, the slowing-down and runaway mean times, and the energy limit probability. Here, we present a novel backward MC approach to these problems based on backward stochastic differential equations that describe the dynamics of the runaway probability by means of the Feynman-Kac theory. The key ingredient of the backward MC algorithm is to place all the particles in a runaway state and simulate them backward from the terminal time to the initial time. As such, our approach can provide much faster convergence than direct MC methods (by significantly reducing the number of particles required to achieve a prescribed accuracy) while at the same time maintaining the advantages of particle-based methods (compared to continuum approaches). The proposed algorithm is unconditionally stable and can be parallelized as easy as the direct MC method, and its extension to dimensions higher than two is straightforward, thus paving the way for conducting large-scale RE simulation.
Publications:
- G. Zhang, and D. del-Castillo-Negrete, A backward Monte-Carlo method for time-dependent runaway electron simulations, Physics of Plasmas, 24 (2017), pp. 092511.
- E. Hirvijoki, C. Liu, G. Zhang, D. del-Castillo-Negrete, and D. Brennan, A fluid-kinetic framework for self-consistent runaway-electron simulations, Physics of Plasmas, 25 (2018), pp. 062507.
Significance and Impact
- It has shown impact on predicting probabilities of runaway electrons (REs), which is a major threat to nuclear fusion tokamaks.
- This method bridges kinetic simulation codes for electrons and fluid codes for background plasmas, to establish a comprehensive RE simulation environment.
- This method achieves higher accuracy with significantly less cost, when comparing to Monte Carlo (MC) methods.
Last Updated: January 14, 2021 - 4:31 pm