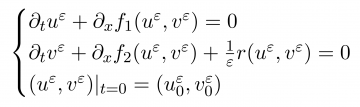
Achievement
We show the convergence of the zero relaxation limit of 2 x 2 systems of hyperbolic balance laws with stochastic initial data. Precisely, solutions converge to a solution of the local equilibrium approximation as the relaxation time tends to zero. The initial data are assumed to depend on finitely many random variables, and the convergence is then proved via the appropriate analogues of the compensated compactness methods used in treating the deterministic case. We also demonstrate the validity of this limit in the case of the semi-linear p-system; the well-posedness of both the system and its equilibrium approximation are proved, and the convergence is shown with no a priori conditions on solutions. This model serves as a prototype for understanding how asymptotic approximations can be used as control variates for hyperbolic balance laws with uncertainty.
Last Updated: January 15, 2021 - 2:12 pm