Achievement
We designed a new algorithm for performing NMF on sparse data which can exploit the structured sparsity. We call our new algorithm multi-frontal NMF (Mf-Nmf), since it borrows several ideas from the multi-frontal method for unconstrained factorization (e.g. LU and QR). We also present an efficient shared memory parallel implementation of Mf-Nmf and discuss its performance and scalability. We conduct several experiments on synthetic and real-world datasets and demonstrate the usefulness of the algorithm by comparing it against standard baselines.
Significance and Impact
Non-negative matrix factorization(Nmf) is the problem of determining two factor matrices W and H for the given input matrix A such that the product WH closely approximates A. It is an important tool in high-performance large scale data analytics with applications ranging from community detection, recommender system, feature detection and linear and non-linear unmixing. While traditional NMF works well when the data set is relatively dense, however, it may not extract sufficient structure when the data is extremely sparse. Specifically, traditional NMF fails to exploit the structured sparsity of the large and sparse data sets resulting in dense factors. The Mf-NMF algorithm can exploit the structured sparsity that allows researchers to better understand the sparse data composition. Also, the Mf-Nmf algorithm is also more parallel than the traditional NMF, thereby enabling efficient analysis of large and sparse datasets. The Mf-Nmf algorithm is faster by 1.2x to 19.5x on 24 cores with an average speedup of 10.3x across all the real-world datasets when compared to an efficient NMF implementation.
Research Details
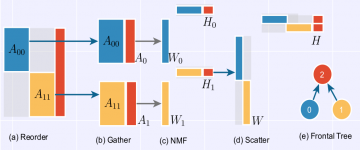
For sparse input matrices A, we need sparse W and H non-negative factors to approximate. Still, the reconstruction error with the sparse factors will be high, that is., in the order of 0.8 and 0.9. This is because, the low-rank approximation obtained out of product WH will have non-zero entries in the place of zeros on the input matrix A, resulting in huge error. That is., number of non-zeros on product WH is much greater than number of non-zeros on A. To overcome this problem, the proposed Multifrontal Non-negative Matrix Factorization(Mf-Nmf) algorithm constructs the sparse factors matrices, considering only the denser non-zeros blocks obtained by reordering and partitioning the input matrix A.
Publication
Sao, Piyush, Ramakrishnan Kannan, ”Multifrontal non-negative matrix factorization" In Proceedings of the International Conference on parallel processing and applied mathematics 2019 (PPAM’19, to appear)
Overview
Non-negative matrix factorization(Nmf) is an important tool in high-performance large scale data analytics with applications ranging from community detection, recommender system, feature detection and linear and non-linear unmixing. While traditional NMF works well when the data set is relatively dense, however, it may not extract sufficient structure when the data is extremely sparse. Specifically, traditional NMF fails to exploit the structured sparsity of the large and sparse data sets resulting in dense factors. We propose a new algorithm for performing NMF on sparse data that we call multi- frontal NMF (Mf-Nmf) since it borrows several ideas from the multi-frontal method for unconstrained factorization (e.g. LU and QR). We also present an efficient shared memory parallel implementation of Mf-Nmf and discuss its performance and scalability. We conduct several experiments on synthetic and realworld datasets and demonstrate the usefulness of the algorithm by comparing it against standard baselines. We obtain a speedup of 1.2x to 19.5x on 24 cores with an average speed up of 10.3x across all the real world datasets.
Last Updated: January 15, 2021 - 11:46 am