Highlight

A Feynman-Kac based numerical method for the exit time probability of a class of transport problems

exit-2d
The exit probability for a 2D advection-diffusion problem. Each pixel represents the probability of a particle (departing from the location of the pixel) exiting the domain by a given time T.

Achievement

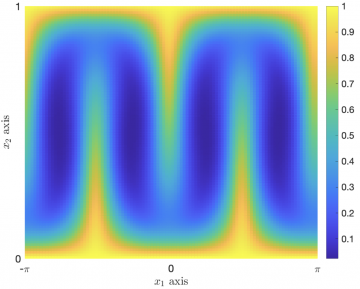
The exit time probability, which gives the likelihood that an initial condition leaves a prescribed region of the phase space of a dynamical system at, or before, a given time, is arguably one of the most natural and important transport problems. Here we present an accurate and efficient numerical method for computing this probability for systems described by non-autonomous (time-dependent) stochastic differential equations (SDEs) or their equivalent Fokker-Planck partial differential equations. The method is based on the direct approximation of the Feynman-Kac formula that establishes a link between the adjoint Fokker-Planck equation and the forward SDE. The Feynman-Kac formula is approximated using the Gauss-Hermite quadrature rules and piecewise cubic Hermite interpolating polynomials, and a GPU accelerated matrix representation is used to compute the entire time evolution of the exit time probability using a single pass of the algorithm. The method is unconditionally stable, exhibits second order convergence in space, first order convergence in time, and it is straightforward to parallelize. Applications are presented to the advection diffusion of a passive tracer in a fluid flow exhibiting chaotic advection, and to the runaway acceleration of electrons in a plasma in the presence of an electric field, collisions, and radiation damping. Benchmarks against analytical solutions as well as comparisons with explicit and implicit finite difference standard methods for the adjoint Fokker-Planck equation are presented.

Publication:

  • M. Yang, G. Zhang and D. del-Castillo-Negrete and M. Stoyanov, A Feynman-Kac based numerical method for the exit time probability of a class of transport problems, Journal of Computational Physics, 444, pp. 110564, 2021. 

Significance and Impact

  • The unconditional stability for any ∆t, first-order convergence with respect to ∆t, and second-order convergence with respect to ∆x.
  • The output of our method can be used to obtain the exit probability of the SDE with different initial conditions by doing simple convolution.
  • Recovering the entire dynamics of the exit probability P(t, x) by only one temporal iteration, and easy implementation on GPUs.

Last Updated: August 4, 2021 - 9:11 am

Sponsors