Highlight

Computational Complexity of Neuromorphic Algorithms

Neuromorphic Sorting Algorithm
Neuromorphic algorithm for sorting a list of natural numbers. The numbers x_1 through x_N are encoded in the delays of synapses going from the source neuron (neuron 0) to the target neurons. The target neurons spike in the order of sorted numbers. This is a pseudo-polynomial time algorithm, i.e. it is linear in value of the inputs, but exponential in size of the inputs.
2021: Q4

Achievement

Paper titled "Computational Complexity of Neuromorphic Algorithms" accepted at the International Conference on Neuromorphic Systems (ICONS) 2021.

Significance and Impact

Neuromorphic computing has several characteristics that make it an extremely compelling computing paradigm for post Moore computation. Some of these characteristics include intrinsic parallelism, inherent scalability, collocated processing and memory, and event-driven computation. While these characteristics impart energy efficiency to neuromorphic systems, they do come with their own set of challenges. One of the biggest challenges in neuromorphic computing today is to establish the theoretical underpinnings of the computational complexity of neuromorphic algorithms. Today, we are unable to compare neuromorphic algorithms to their conventional counterparts that run on CPUs and GPUs because we are missing a framework that can be used to talk about the computational complexity of neuromorphic algorithms. If we devise such a framework, we can directly compare neuromoprhic algorithms to their conventional counterparts. This will enable us to talk about neuromophic algorithms not only in terms of their energy efficiency, but also in terms of the running time and space complexity. This line of research would compel us to develop radically different neuromorphic algorithms that convincingly outperform conventional algorithms.

Research Details

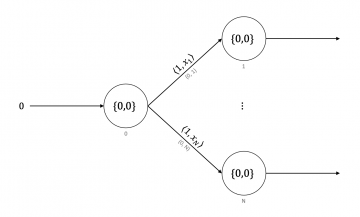
In this paper, we take the first steps towards defining the space and time complexity of neuromorphic algorithms. Specifically, we describe a model of neuromorphic computation and state the assumptions that govern the computational complexity of neuromorphic algorithms. Next, we present a theoretical framework to define the computational complexity of a neuromorphic algorithm. We explicitly define what space and time complexities mean in the context of neuromorphic algorithms based on our model of neuromorphic computation. Finally, we leverage our approach and define the computational complexities of six neuromorphic algorithms: constant function, successor function, predecessor function, projection function, neuromorphic sorting algorithm and neighborhood subgraph extraction algorithm.

Last Updated: August 31, 2021 - 11:03 am

Sponsors