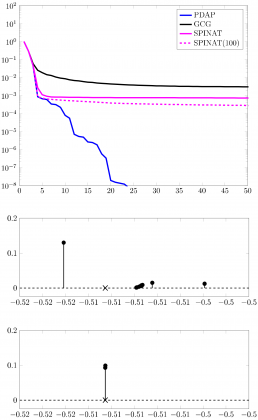
The steps of the new method (blue) approach the optimal solution at a guaranteed rate, while previous methods effectively stagnate: the classical GCG method (black) and other acceleration methods (magenta).
Bottom: Acceleration avoids clustering. The optimal configuration computed with existing methods form clusters (bottom upper plot), which causes an artificially inflated number of Dirac-deltas. The new method accurately detects the optimal locations (bottom lower plot).
Achievement
An improved approach for solving certain classes of nonconvex optimization problems with an unknown number of optimization variables is developed. The method relies on a reformulation of the problem as a sparse optimization problem over a space of discrete measures, which are sums of Dirac-delta peaks characterized by their location in space and an associated coefficient.
The optimal solution is computed via a two-step procedure: an outer loop that iteratively inserts and removes peaks and an inner loop that determines the optimal solution of a convex optimization sub-problem with a fixed number of variables.
Significance and Impact
The optimization problems addressed in this work arise in various application domains, such as optimal sensor placement, inverse source detection, and compressed sensing with continuous dictionaries. This work describes an improved algorithm for solving these nonconvex optimization problems through a procedure that requires to compute simple insertion steps and an accurate resolution of convex sub-problems with a small number of optimization variables with readily available solvers.
The new method is able to solve the problems more accurately in fewer steps, reduces computational clustering artifacts known to affect existing methods, and is backed up by a rigorous convergence analysis.
Research Details
- A very general optimization framework is presented together with several examples of relevance that can be solved with it.
- An overview over existing solution methods based on a reformulation using sparse measures and generalized conditional gradient methods is given and the proposed acceleration strategy is outlined.
- The mathematical analysis shows that the accelerated methods can solve the problem up to a guaranteed precision with a linear convergence rate, whereas existing methods only converge at a much slower sub-linear rate.
- The analysis also shows how the new method is able to reduce computational artifacts that affect existing methods.
- Computational experiments confirm that the accelerated methods perform better in practice and demonstrate that the analysis accurately reflects the practical behavior.
Overview
A class of generalized conditional gradient algorithms for the solution of optimization problem in spaces of Radon measures is presented. The method iteratively inserts additional Dirac-delta functions and optimizes the corresponding coefficients. Under general assumptions, a sub-linear rate in the objective functional is obtained, which is sharp in most cases. To improve efficiency, one can fully resolve the finite-dimensional subproblems occurring in each iteration of the method. We provide an analysis for the resulting procedure: under a structural assumption on the optimal solution, a linear convergence rate is obtained locally.
Last Updated: January 14, 2021 - 7:29 pm